Introduction

The GIST index is a balanced tree, but that’s basically the only thing that it has in common with a BTree.

One of its particularity is that it can be extended to any type of data as long as a few functions implemented. I will mention these function in this article, and if you want to go further, you can go read the GiST indexing Project website

But for now we are going to focus on a few usecases, and not list all the extensions that great people have made for GiST :)

So after the last article, our birds dentists were able to look for certain syndroms and also find the most urgent appointments. All of this helping them organise their day. But what they need, is to do a schedule of course ! So in order to do that, they want to find which crocodile took an appointment when they are free.

So here we are, we have a problem of data overlapping. And so we create the following index

CREATE INDEX ON appointment USING GIST(schedule)

And of course, let’s first talk about the internal data structure

A quick word about the gevel extension

TODO

GiST structure

So, as I said, the GiST index is also a balanced tree. If you have a doubt on what an balanced tree is, you can read the article on BTree.

As in a BTree, the keys in a GiST are a tuple (value, pointer). The main difference with a BTree index, the data isn’t ordered in the pages. And the key ranges of the pages can overlap. This means that a tuple could potentially fit in different pages.

In order to be able to visualise the data in a GiST index, I used the extension Gevel.

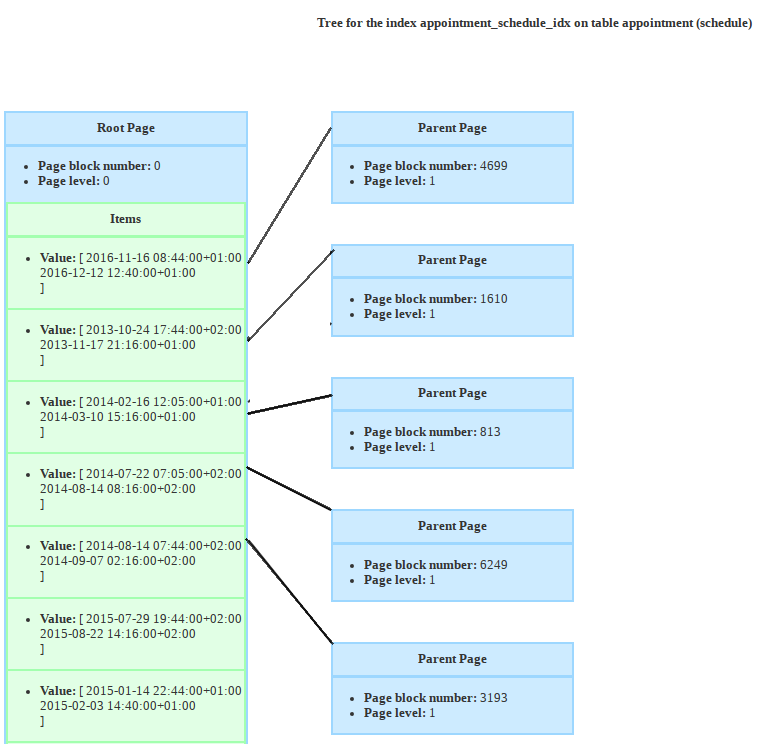
Here is only the root level and its children (I didn’t display the items for readability). But what you can see is that, indeed, the items are not ordered like in a BTree.

Moreover if you zoom in, you can see that, if we wanted to insert an appointment scheduled from August 14th 2014 at 7:30am to 8:30am, if could fit in both branches (circled in red) of the tree.

The rest of the structure of a GiST index is quite close to the BTree, the leaf pages have pointers to the heap tuples in the table. There is nothing quite fancy to explain except the values in the pages overlapping and unordered.

But I believe that it will become clearer why a GiST index has such odd values if we talk about the search algorithm.

Searching in a GiST index

Let’s say that we have a bird that hasn’t schedule any appointment on a morning and wants to see the appointments overlapping that period as he’s not super strict about the start and finish time.

Here is the result of the query

croco_new=# SELECT c.email, schedule, done, emergency_level
            FROM appointment
            INNER JOIN crocodile c ON (c.id=crocodile_id)
            WHERE schedule && '[2018-05-17 08:00:00, 2018-05-17 13:00:00]'::tstzrange
            AND done IS FALSE ORDER BY emergency_level DESC LIMIT 5;
-[ RECORD 1 ]---+----------------------------------------------------
email           | louise.choudhuri238732@croco.com
schedule        | ["2018-05-17 12:03:00+02","2018-05-17 13:03:00+02")
done            | f
emergency_level | 9
-[ RECORD 2 ]---+----------------------------------------------------
email           | louise.romano225288@croco.com
schedule        | ["2018-05-17 08:30:00+02","2018-05-17 09:30:00+02")
done            | f
emergency_level | 9
-[ RECORD 3 ]---+----------------------------------------------------
email           | david.chakma246035@croco.com
schedule        | ["2018-05-17 08:40:00+02","2018-05-17 09:40:00+02")
done            | f
emergency_level | 9
-[ RECORD 4 ]---+----------------------------------------------------
email           | pablo.galli249346@croco.com
schedule        | ["2018-05-17 08:40:00+02","2018-05-17 09:40:00+02")
done            | f
emergency_level | 9
-[ RECORD 5 ]---+----------------------------------------------------
email           | harry.rizzi254582@croco.com
schedule        | ["2018-05-17 09:22:00+02","2018-05-17 10:22:00+02")
done            | f
emergency_level | 9

Without a GiST index, what postgres uses is an index scan and check if each row has a common point with the value [2018-05-17 08:00:00, 2018-05-17 13:00:00].

This is what you see when you look into the EXPLAIN from the query.

QUERY PLAN
-------------------------------------------------------------------------------
 Limit  (cost=... rows=5 width=56)
   ->  Sort  (cost=... rows=102 width=56)
         Sort Key: appointment.emergency_level DESC
         ->  Nested Loop  (cost=... rows=102 width=56)
               ->  Seq Scan on appointment
                   (cost=... rows=102 width=31)
                      Filter: ((done IS FALSE)
                      AND (schedule && '["2018-05-17 08:00:00+02",
                                         "2018-05-17 13:00:00+02"]'::tstzrange))
               ->  Index Scan using crocodile_pkey on crocodile c
                   (cost=... rows=1 width=33)
                     Index Cond: (id = appointment.crocodile_id)
(10 lignes)

With a GiST index, in the EXPLAIN the index is used. As the query plan is a bit long, here is the line where you can see it.

->  Bitmap Heap Scan on appointment  (cost=... rows=123 width=31)
      Recheck Cond: (schedule && '["2018-05-17 08:00:00+02",
                                   "2018-05-17 13:00:00+02"]'::tstzrange)
      Filter: (done IS FALSE)
      ->  Bitmap Index Scan on appointment_schedule_idx  (cost=... rows=246 width=0)
            Index Cond: (schedule && '["2018-05-17 08:00:00+02",
                                       "2018-05-17 13:00:00+02"]'::tstzrange)

The search algorithm for GiST also uses scan keys. If scan keys are new to you, you can read about them in the first article of this serie.

Once scan keys are initialised, the function gistgetbitmap returns a bitmap of all the heap tuple pointers (tids) matching the scan keys.

To do that the GiST tree is explored starting from the root.

The function GistScanPage scans the items from a page.

As in a BTree search, it checks if there was a page split caused by a concurrent insert. The difference is that, as the items are unordered and can overlap, if there was a page split, both pages can contain tuples matchin the scan key. So, the right sibling is added to a queue of pages to explore. In a BTree, it simply moves to the right sibling.

Then for each item of the page, if it’s not marked as deleted, we check thanks to the gistindex_keytest function if the item matches the scan key.

This function calls the method Consistent that has to be implemented for the key class that you want to index. This methods returns NO If the tree page can’t contain the scan key from the query, else MAYBE. In the cases of ranges or geometries the Consistent method checks if the scan key overlaps the item value. That’s why GiST indexes are very efficient for overlapping, ranges containing data, or geographic data with GIS (like if I wanted to check if two geographic areas overlap)

If the item matches and the page is a leaf page, the pointer is the TID of a heap tuple in the table, so it’s added to the tuples bitmap. If the scan is ordered. The distance from the scankey if evaluated thanks to the Distance function, that is a key class function.

Else, if the page is not a leaf page, the item is pushed in a seach queue. The page pointed by the item will then be recursively explored.

Let’s go back to our query. So if we are looking for the rows overlapping the period ‘[2018-05-17 08:00:00, 2018-05-17 13:00:00]’, as you can see in the following figure, there are two items in the root (at least, I didn’t look into ALL the root items) that could lead to leaves with matching rows. So this branches are going to be explored recursively until the leaves.

It’s also important to note that the key class defines a Distance function. This function is used if in the query there was an ORDER BY like here.

croco_new=# SELECT c.email, schedule, done, emergency_level
            FROM appointment
            INNER JOIN crocodile c ON (c.id=crocodile_id)
            WHERE schedule && '[2018-05-17 08:00:00, 2018-05-17 13:00:00]'::tstzrange
            AND done IS FALSE ORDER BY schedule DESC LIMIT 3;
-[ RECORD 1 ]---+----------------------------------------------------
email           | harry.yoon348422@croco.com
schedule        | ["2018-05-17 12:55:00-07","2018-05-17 13:55:00-07")
done            | f
emergency_level | 5
-[ RECORD 2 ]---+----------------------------------------------------
email           | alfred.ferrara349165@croco.com
schedule        | ["2018-05-17 12:55:00-07","2018-05-17 13:55:00-07")
done            | f
emergency_level | 3
-[ RECORD 3 ]---+----------------------------------------------------
email           | harry.das285454@croco.com
schedule        | ["2018-05-17 12:44:00-07","2018-05-17 13:44:00-07")
done            | f
emergency_level | 1

To sum up

The search has to explore all the tree branches that overlap the scan key we are looking for. To do that it’s using a bitmap and comparing the scan key with the Consistent key class function.

Inserting a new tuple

As I said earlier, a tuple can be inserted in several different leaf pages, it could actually be inserted anywhere in the tree but that would be very bad for the search performance.

gistdoinsert handles inserts. In order to insert a new tuple, it will start from the root and descend the tree following the smallest “Penalty”.

So, recursively, until the page is a leaf, it’s going to:

Step 1: Check for page split

First, if there was a concurrent page split, the current page might not be the best path anymore. So in case of page split, the algorithm recurses back to the current page parent.

Step 2: find the best path

The function gistdoinsert calls the function gistchoose which finds the best tree branch to follow, meaning the best page child page of the current one.

To do that, gistchoose goes over the items of the current page, it will calculate the penalty. Penalty is a key class function. It gives a number representing how bad the value to insert would fit in the child page.

If it’s a multicolumn index, it will calculate the penalty of each column.

Step 3: updating or inserting

Once the right page is found, the function gistinserttuples is called. It will either insert the tuple if it’s a leaf or update the value if it’s a parent.

It’s gistplacetopage that handles the two cases (update or insert).

Update

Indeed, it can be necessary to update the key in a parent level if the range changed. For example, let’s say I insert an appointment with the schedule value [2013-11-20 05:30:00, 2013-11-20 06:30:00]. As you can see in the following images, the range of the page where it was inserted changed which led to an update of the value in the root page.

The key class function Union is used to find the new range.

Insert

If we reached the leaf page, it’s time to insert. gistplacetopage checks if there is enough space in the page to insert the tuple. If there is, it simply inserts it and we’re done as the parent levels were already updated with the union key.

But if there is not enough space, a page split is necessary. Page splits in a GiST index are different from splits in a BTree. In a BTree, basically, 50% of the old page is moved to the new one. As the data is ordered, there is not much to do to decide what should go on the right and the left page. In a GiST, we want to make groups of items with little distance to then optimise search.

To do that, each key class defines a PickSplit method. PickSplit decides which items stay on the old page and which ones will be on the new one.

In case of page split, it becomes necessary to recurse in the parent level to insert a new item with a pointer to the new page. Of course this can also generate a page split.

On the following pictures you can see that after a page split, the new page becomes the rightmost page and the range of the old page changed.

To sum up

In order to insert GiST follows the path with the least penalty updating on its way the parents keys.

I’d say that it’s important to remember that the functions Union, Penalty and PickSplit are key class function.

GiST or GIN for a fulltext search

TODO

To sum up

Union Distance Consistent Penalty PickSplit